Работа с детьми. Дифференцированный подход

Развитие логического мышления детей – процесс длительный и весьма трудоемкий; прежде всего для самих детей – уровень мышления каждого очень специфичен.

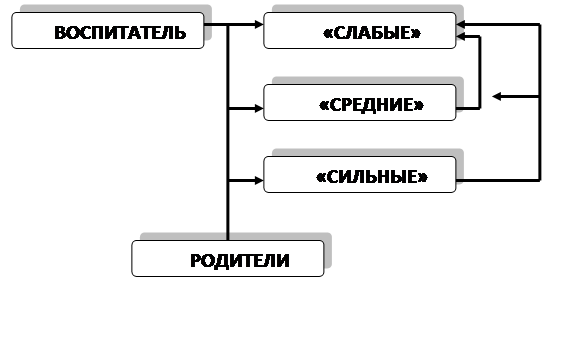
Мысленно я распределяю детей на три группы:

Такое разделение помогает ориентироваться в подборе занимательного материала и задач, предупреждает возможные перегрузки «слабых» детей, потерю интереса (ввиду отсутствия усложнений) – у «сильных»

Детям, справляющимся с логическими задачами на среднем уровне, я предлагаю варианты подобных задач, а так же подключаю к играм соревновательного характера.

Особый подход необходим к «слабым» детям. Учитывая их психические и физические особенности, я стараюсь внушить им уверенность в себе, подвести к самостоятельному решению простых задач. В случае быстрого утомления, вид деятельности сменяется. С родителями ведется широкая консультационная работа. Особую роль играют «сильные» дети: отлично справившись с конкретной задачей они, по моей просьбе (или самостоятельно) «подключаются» к тем, кто испытывает серьезные трудности.

Такая форма взаимодействия педагога и воспитанников очень эффективна. Она помогает сплотить коллектив, дает возможность самоутвердиться успевающим детям и почувствовать уверенность в своих силах – более слабым.

Познавательно о обучении:

Обмен углеводов и его нарушения
Углеводы составляют незначительную часть общего сухого веса тканей человеческого организма - не более 2%, в то время как на белки, например, приходится до 45% сухой массы тела. Тем не менее, углеводы выполняют в организме целый ряд жизненно важных функции, принимая участие в структурной и метаболич ...

Педагогические приемы активизации самостоятельной деятельности учащихся на занятиях по Дальтон-технологии
Нестандартные формы занятий, предусмотренные в самой Дальтон-технологии: занятие-погружение, занятие-консультация, занятия-лекции, интегрированные занятия, проектные занятия, групповые и индивидуальные занятия. Применение игровых форм занятий: ролевые, организационно-деятельностные, имитационные. П ...

Возникновение воспитания. Воспитание как общественное явление
Педагогика как наука сформировалась значительно позже, чем появилось в человеческом обществе то, что она изучает – воспитание. Когда же возникло воспитание? Это не простой вопрос, на который давно пытаются ответить различные отрасли человеческого знания, и прежде всего философия, история, этнографи ...