Подготовка плана электронных учебных материалов

Новая педагогика » Методика разработки и использования средств информационно-коммуникационных технологий для формирования геометрической компетентности учащихся основной школы » Подготовка плана электронных учебных материалов

Страница 10

Исследование модели.

С помощью геометрических теорем необходимо доказать, что построенный отрезок PQ действительно является перпендикуляром к прямой a.

Задача.

Дан неразвернутый угол A. Построить его биссектрису. Формальная модель.Построим формальную модель процесса геометрического построения, зафиксировав его в форме алгоритма: Смотрите подробности курсы по HTML для подростков Владивосток на сайте.

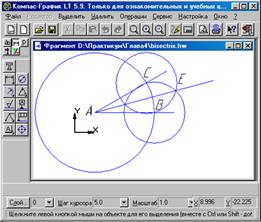
1. Построить окружность произвольного радиуса с центром в вершине заданного угла А, которая пересечет стороны угла в точках В и С.

2. Построить две окружности радиуса ВС с центрами в точках B и C. Точку пересечения окружностей внутри угла обозначить буквой Е.

3. Через вершину угла А и точку пересечения окружностей Е провести прямую. Луч АЕ – биссектриса заданного угла.

Компьютерная модель.

Реализуем геометрическое построение в соответствие с разработанным алгоритмом с использованием системы КОМПАС-3D.

	Построение биссектрисы неразвернутого угла.
1	Построить неразвернутый угол и окружность с центром в точке А (вершине угла). На панели Геометрические построения щелкнуть по кнопке Ввод отрезка и построить два отрезка, выходящих из точки А. Щелкнуть по кнопке Ввод окружности и в автоматическом режиме построить окружность произвольного радиуса с центром в точке А.
2	Ввести обозначения точек пересечения окружности. Активизировать панель Размеры и технологические обозначения, щелкнуть по кнопке Ввод текста и ввести обозначения вершины угла А и точек пересечения окружности со сторонами угла В и С.
3	Построить две окружности одинакового радиуса с центрами в точках В и С. Задать радиусы окружностей в ручном режиме. Точку пересечения окружностей обозначить E.
4	Через вершину угла А и точку пересечения окружностей Е провести прямую. Щелкнуть по кнопке Ввод отрезка и в автоматическом режиме последовательно указать точки А и Е.
7	Алгоритм построения биссектрисы неразвернутого угла выполнен.
8	Сохранить чертеж.

Исследование модели.

С помощью геометрических теорем необходимо доказать, что построенный луч АЕ действительно является биссектрисой угла А.

Таким образом, демонстрируется возможность использования средств ИКТ для решения геометрических задач.

Страницы: 5 6 7 8 9 10

Познавательно о обучении:

Психологический и физиологический аспекты адаптации ребенка к школе
Младший школьный возраст – важный период в жизни ребенка, в котором происходят формирование личности, развитие личностных механизмов поведения, начальный школьный период жизни является периодом наиболее интенсивного и нравственного развития, когда закладывается фундамент физического, психического и ...

Обзор образовательной программы по экологическому воспитанию для детей дошкольного возраста
Развитие экологического образования как нового направления дошкольной педагогики в нашей стране началось гораздо позже, чем экологического образования школьников и студентов. Несмотря на это, в настоящее время именно дошкольное звено в системе непрерывного экологического образования работает наибол ...

Современный подход новых программ и методик.
В настоящее время многие современные программы дошкольного образования акцентируют свое внимание на ребенке, как на неповторимой, творчески развивающейся личности. Немаловажную роль уделяется и уровню мыслительной деятельности дошкольника. Очень сильной и серьезной программой, ориентирующейся на ра ...

Подготовка плана электронных учебных материалов

Категории