Подготовка плана электронных учебных материалов

- давать возможность учащемуся контролировать динамику процесса конструирования модели, задавая режимы изменения параметров;

- давать возможность управлять позицией наблюдателя при зрительном исследовании модели;

- давать возможность отбора наиболее приемлемых с психолого-педагогической точки зрения соотношения размеров модели из большого числа экспериментальных данных;

- позволять выборочно стирать изображение;

- давать возможность учащимся достраивать модель;

- проводить дублирование изображений;

- позволять проводить анализ корректности вводимых данных;

- сопровождать модели интеллектуализированным диалогом, в ходе которого будут вводиться термины, обозначающие элементы модели, давать поясняющие сообщения.

Важное место в работе с моделями занимают упражнения на развертки различных фигур. Многие программы выводят различные плоскостные конфигурации, а учащимся предлагается узнать, какие из них являются развертками той или иной фигуры.

Пространственные соотношения между реальными объектами (положение и ориентация объектов в пространстве и их размеры) изучаются с помощью геометрических моделей. Для визуализации геометрических моделей используются идеализированные геометрические объекты (точка, линия, плоскость и др.), которые в отличие от реальных объектов обладают набором только наиболее существенных свойств. Так геометрическая точка отличается от реальной точки на чертеже тем, что имеет только координаты, но не имеет размеров, геометрическая линия не имеет ширины, геометрическая плоскость - толщины и т.д. В школьном курсе геометрии не только изучаются различные геометрические модели (теоремы), но рассматривается процесс их построения. Важное место занимают геометрические построения с использованием линейки и циркуля. Для создания геометрических моделей на компьютере удобно использовать системы автоматизированного проектирования (САПР). В качестве примера выполнения геометрического построения рассмотрим задачу о построении перпендикуляра к прямой.

Задача.

Даны прямая и точка на ней. Построить прямую через данную точку и перпендикулярную к данной прямой. Формальная модель.

Построим формальную модель процесса геометрического построения, зафиксировав его в форме алгоритма:

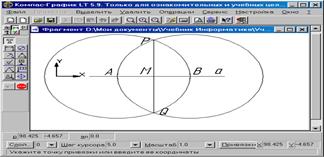
1. Построить прямую a и точку M на ней.

2. На равных расстояниях от точки М построить на прямой точки А и В.

3. Построить две окружности с центрами в точках A и В с радиусом АВ.

4. Через точки пересечения окружностей P и Q провести прямую. Данная прямая пройдет через точку М и будет являться перпендикуляром к прямой a.

Компьютерная модель.

Реализуем геометрическое построение в соответствие с разработанным алгоритмом с использованием системы КОМПАС-3D.

Познавательно о обучении:

Общая характеристика внеучебной деятельности
Под внеучебной деятельностью понимается активное взаимодействие педагога с детьми, направленное на достижение определенных воспитательных целей. В процессе организации внеучебной деятельности у учащихся формируются предусмотренные новообразования или развиваются ранее приобретенные. В процессе их к ...

Педагогические основы развития технологической культуры учащихся
Для того чтобы сформулировать активизацию учебно-преобразовательной деятельности учащихся, используется весь арсенал методов организации и осуществления учебной деятельности - словесные, наглядные и практические методы, репродуктивные и поисковые методы, индуктивные и дедуктивные методы, а также ме ...

Управляемая система. Содержание воспитания
Процесс воспитания является стержневым в формировании человека. В результате проблемного анализа педагогическим коллективом выделены основные направления деятельности в содержании воспитания через среды воспитательной системы школы: · гражданско – патриотическое воспитание и краеведение; · экологич ...