Методика работы по раскрытию софизмов

6. «Правило программиста».

Работа блоками. Невозможно отлаживать программу в целом. Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока.

Предложенные рекомендации с одной стороны помогут ученикам при разборе софизмов, с другой стороны будут способствовать обогащению набора приёмов самопроверки и самоконтроля. Самая актуальная информация финансовый сервис кредитный брокер здесь.

Наряду с упражнениями по раскрытию софизмов можно предложить ученикам задания по составлению софизмов. С такого рода заданиями ученики сталкиваются впервые. Обычно за ошибки, допущенные в решении, их наказывали, а здесь, наоборот, требуется умышленно допустить ошибку, да ещё при этом сделать так, чтобы её не сразу можно было найти. Парадоксальность ситуации вызывает интерес со стороны учеников, и они охотно берутся за выполнение задания. Главная цель таких заданий способствовать более осознанному усвоению изучаемого материала и развитию творческого мышления.

На первом этапе можно дать такое задание: «Решить упражнение (пример, задачу, уравнение и т.д.) с ошибкой». Его можно предложить в качестве творческого домашнего задания, которое выполняется на отдельных листочках. Далее ученики могут обменяться своими решениями и попытаться найти ошибки друг у друга. Учитель собирает все работы, проверяет их и самые интересные демонстрирует всему классу. На втором этапе сообщаем ученикам, что многие из тех ошибок, которые они допускают, используются для составления доказательств заведомо ложных утверждений, т.е. софизмов. На третьем и этапе можно предложить ученикам решить задание с ошибкой, более или менее её замаскировав, и получить отсюда какой-либо неверный вывод.

Проанализировав соответствующую литературу и задачники, содержащие софизмы, можно прийти к выводу, что, во-первых, из всего множества софизмов далеко не каждый можно использовать на уроке, а, во-вторых, в литературе нет строгого разделения ошибочных рассуждений на те, которые можно использовать во внеклассной работе и те, которые подойдут для урока.

Поэтому выделяют несколько способов составления доказательств ложных рассуждений.

1. Для составления софизмов можно использовать ученические ошибки. Действительно, некоторые ошибки, скрытые в софизмах, ученики зачастую допускают сами. Знание учителем типичных ошибок позволит ему составлять разнообразные, интересные, а главное, «рабочие» софизмы.

Например, докажем, что 3 > 5, используя следующую ошибку: при делении обеих частей неравенства на отрицательное число не сменили знак неравенства на противоположный.

3 > 2; \·2

3∙2 > 2²; \+ (3²)

3∙2 - 3² > 2² - 3²;

3·(2 - 3) > (2 - 3)·(2 + 3);

3 > 2 + 3;

3 >5.

Обычно, учитель говорит: «Неверно», «Так нельзя», но, как правило, долговременного эффекта это не даёт.

2. Учитель может использовать для составления софизмов те психологические закономерности усвоения и запоминания материала, о которых уже говорилось выше. В частности, он может составлять доказательства ложных утверждений используя неточные определения, неполные формулировки, ошибочные выводы, обратные теоремы, которые неверны. К примеру, «забыв», что переход , возможен только при a > 0,m € Z, n € N, n, то можно получить следующее:

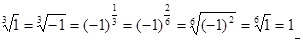
Таким образом, доказывается, что -1 = 1.

Этот опыт и фантазия учителя, наверняка подскажут ему подобные задания по различным темам.

3. Использование «обманных» или провоцирующих задач. Под «обманными» задачами понимают задачи, в которых условие либо противоречиво, либо решение невозможно при конкретных данных, либо они имеют ещё какой-либо недостаток, сводящий задачу на «нет» и делающий её абсурдной по сути.

Обычно обманная задача не требует решения, но если попытаться её решить, то можно получить какой-либо абсурдный вывод. Таким образом, мы получим некоторый софизм. После предъявления такой задачи возможно два варианта событий. Ученики заметят подвох и не станут решать задачу, тогда учитель покажет к чему бы они пришли, если бы, всё таки попытались её решить. В этом случае, у учеников возникнут положительные эмоции по поводу того, что они вовремя заметили скрытую ошибку и не «попались в ловушку». Но ученики могут и ничего не заметить, и тогда учитель подводит их к нелепому результату, выясняется причина такого результата. А в этом случае у школьников возникает чувство досады на себя из-за невнимательности, из-за того, что они угодили в ловушку, причём заранее подготовленную. Но в любом случае эмоциональная окраска ситуации способствует осознанию значимости, важности данного материала, повышению интереса учащихся к предмету, что в свою очередь влияет на сознательность и прочность усвоения учебного материала.

Познавательно о обучении:

Приемы стимулирования учебной деятельности младших школьников
Развитию мотивации необходимы стимулирующая среда и целенаправленное влияние через систему педагогических приемов. Среди множества приемов по изучению и развитию мотивации можно выделить следующие. 1. Дети отличаются любопытством. Они проявляют особенный интерес к новым и неизвестным обстоятельства ...

Дифференцированная система оценивания знаний, умений и навыков учащихся на уроках - зачетах
Изменение подходов к контролю совершенно естественно влечет за собой мысль о целесообразности изменения системы оценивания. Дело в том, что достижение учеником уровня обязательной подготовки неизбежно может быть оценено только по двухбалльной шкале. Поэтому естественно для достигших учеником уровня ...

Врачебно-педагогическая характеристика школьников с ослабленным здоровьем
Основным критерием отбора в различные группы является состояние здоровья учеников. Определяет соответствующую группу врач при обязательном участии педагога. При оценке состояния здоровья школьников следует проверить характер отклонений в деятельности организма. Методика обследования включает следую ...