Джованни Чева

Третьего марта 1648 года в Милане родился будущий итальянский инженер и математик Джованни Чева.

Окончил Пизанский университет. Основные работы по механике, гидравлике и математике.

В 1678 году Джованни Чева доказал теорему о соотношении отрезков некоторых прямых, пересекающих треугольник (Теорема Чевы). Построил учение о секущих, которое положило начало синтетической геометрии: оно изложено в сочинении «О взаимно пересекающихся прямых». Прежде чем сформулировать теорему расшифруем используемое в ней понятие «чевиана» – отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне

Эта теорема гласит: если три чевианы пересекаются в одной точке, то отношения, в которых их основания делят стороны треугольника, удовлетворяют равенство:

.

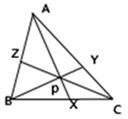
И теорема обратная: Если точки X, Y, Z на прямых, ограничивающих треугольник АВС, удовлетворяют условию Чевы, причём собственно на его сторонах лежат все три либо ровно одна из них, то соответствующие чевианы пересекаются в одной точке или параллельны.

13 декабря 1734 года Джованни Чева скончался в городе Мантуя, в Италии.

Простейший из многоугольников – треугольник – играет в геометрии особую роль. Без преувеличения можно сказать, что вся (или почти вся) геометрия со времен «Начал» Евклида покоится на «трех китах» – трех признаках равенства треугольников. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника». Как о самостоятельном разделе элементарной геометрии.

Познавательно о обучении:

Особенности проведения занятий при деформациях опорно-двигательного аппарата
В данной группе заболёваний наиболее часто встречаются нарушения в формировании позвоночника (нарушение осанки и сколиоз). В большинстве случаев нарушения осанки являются приобретенными. Чаще всего эти отклонения встречаются у детей астенического телосложения, физически слабо развитых. Неправильная ...

Принципы досуга
Всякая деятельность зиждется на общих закономерностях ее развития. Досуг детей, подростков и юношества развивается по своим законам, принципам, теоретически обоснованным и апробированным на практике. К ним относятся: 1. Принцип всеобщности и доступности- то есть возможность приобщения, вовлеченност ...

Особенности гражданского воспитания старшеклассников
Гражданское воспитание старшеклассников - целенаправленный процесс воздействия на учащихся, который должен активно способствовать формированию у них гражданской культуры. Формирование гражданской культуры тесно связано с воздействием массовой информации и переживанием личного опыта участия в гражда ...