Карл Фридрих Гаусс

В Броауншвейге 30 апреля 1777 года родился будущий великий математик. Сын водопроводчика в 1795 году поступил в Геттингенский университет, который с успехом закончил в 1798 году.

В 1799 году Карл Фридрих получил доцентуру в Брауншвейге, а в 1807 году кафедру математики и астрономии в Геттингенском университете.

Немецкий математик, внесший фундаментальный вклад также в астрономию и геодезию, иностранный член – корреспондент (1802) и иностранный, почетный член (1824) Петербургской Академии наук.

Отличительными чертами творчества Гаусса являются глубокая органическая связь в его исследованиях между теоретической и прикладной математикой, необычайная широта проблематики. Работы Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии. Во многих областях математические труды Гаусса содействовали повышению требований к логической отчетливости доказательств, однако сам Гаусс оставался в стороне от работ по строгому обоснованию математического анализа.

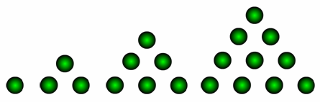
Первое крупное сочинение по теории чисел и высшей алгебре («Арифметические исследования», 1801) во многом предопределило дальнейшее развитие этих дисциплин. В конце книги излагается теория уравнений деления круга (то есть уравнений Хn – 1 =0), которая во многом была прообразом теории Галуа. Помимо общих методов решения этих уравнений Гаусс установил связь между ними и построением правильных многоугольников. Он, впервые после древнегреческих ученых, сделал значительный шаг вперед в этом вопросе, а именно: Гаусс нашел все значения n, для которых правильный n-угольник можно построить циркулем и линейкой. В частности, решив уравнение Х17 – 1 = 0, он дал построение правильного 17-угольника при помощи циркуля и линейки. Гаусс придавал этому открытию большое значение и завещал выгравировать правильный 17- угольник, вписанный в круг, на своем надгробном памятнике, что и было исполнено. Алгебраические интересы Гаусса связаны с основной теоремой алгебры: он дал несколько ее доказательств – первое из них в 1799г. В 1801 немецкий ученый доказал, что всякое натуральное число представимо в виде суммы не более трех треугольных чисел (числа – числа последовательности).

;

;

;

…

Обобщением треугольных чисел являются многоугольные (к-угольные) числа.

В 19 веке роль математической символики возрастает, Гаусс вводит математический знак отношений, например, сравнимости «(mod а)».

Замечательное приложение нашла геометрия в начале 19 века. С ее помощью было измерено все вокруг. В частности, наша Земля. Проблемы геодезии были самыми актуальными проблемами в прикладной математике особенно в первой трети столетия.

Изучение формы земной поверхности потребовало углубленного общего геометрического метода для исследования поверхностей. Выдвинутые Гауссом в этой области идеи получили выражение в сочинении «Общие исследования о кривых поверхностях» (1827). Руководящая мысль этого сочинения заключается в том, что при изучении поверхности как бесконечно тонкой гибкой пленки основное значение имеет не уравнение поверхности в декартовых координатах, а дифференциальная квадратичная форма, через которую выражается квадрат элемента длины и инвариантами которой является все собственные свойства поверхности – прежде всего ее кривизна в каждой точке.

Познавательно о обучении:

Экономическое образование на рубеже веков. Взгляд в будущее
Действительно, развитие российской экономики и экономического образования взаимообусловлено. В этой связи надеяться, экономическое оживление в России окажет благотворное воздействие на становление в стране экономической высшей школы. Рост доходов населения увеличивает платёжеспособный спрос, а стаб ...

Модель концентрированного обучения
Цель концентрированного обучения заключается в ликвидации многопредметности учебного дня, калейдоскопичности ощущений и впечатлений при формировании знаний, раздробленности познания и создания такого процесса обучения, когда вместо шести предметов на шести уроках в течение учебного дня (и четырнадц ...

Применение радио и звукозаписи в работе с детьми
Использование радио в учебной работе детских садов открывает широкие возможности повышения эффективности воспитания и обучения, всестороннего воздействия на личность дошкольника. Центральное радио ежедневно транслирует передачи для дошкольников, которые с успехом можно использовать в учебной работе ...