Якоб Штейнер

Якоб Штейнер родился в 1796 году в Швейцарии в семье крестьянина. В молодости был пастухом. Грамоте Якоб научился лишь в возрасте 19 лет в школе своего знаменитого соотечественника, педагога – демократа Иоганна Генриха Песталоцци (1746–1827).

В общей педагогической системе Песталоцци геометрия как учение о формах занимала особо важное место: ей придавалось исключительное значение в деле общего образования и развития мыслительной деятельности учащихся.

Идеи Песталоцци оказали большое влияние на Штейнера и в дальнейшем склонили его к занятиям синтетической проективной геометрией. Впоследствии, будучи уже членом Берлинской Академии наук, Штейнер в предисловии к важнейшей своей работе «Систематическое развитие зависимости геометрических образов друг от друга» (ч.1, 1896) писал: «Предлагаемое произведение пытается вскрыть тот механизм, которым связаны друг с другом разные разнообразнейшие явления в пространстве. Существует весьма ограниченное количество весьма простых основных соотношений, выражающих ту схему, по которой остальная масса предложений развивается последовательно и без всяких затруднений. Посредством надлежащего усвоения этих немногих основных соотношений делаешься хозяином всего предмета: порядок заступает место хаоса, и видишь, как все части, естественно опираются друг на друга, располагаются в прекрасном порядке и соединяются в удачно ограниченные группы. Таким образом, удается овладеть теми элементами, из которых исходит природа, чтобы с возможной экономией и простейшим образом придать фигурам несчетное множество свойств».

В 1833 году Штейнер охотно изучал построения различными неклассическими средствами. Рассматривались, в частности, построения с помощью двухсторонней линейки, (иными словами разрешалось пользоваться двумя краями линейки), или угольником – прямого угла. Угольник можно было расположить так, что бы его края проходили через данные точки, а вершина попадали на данную линию. Каждое из этих замысловатых приспособлений заменяют циркуль и линейку, причем позволяют получить более простые решения. Если на плоскости нарисован круг с отмеченным центром, выполненный циркулем, то любое построение можно осуществить только линейкой. Другими словами, если задачу можно решить с помощью циркуля и линейки, циркуль достаточно применять только раз. Позднее оказалось, что и от окружности достаточно иметь любую самую малую дугу и центр.

В истории математики С. Л. Лемус остался исключительно потому, что в 1840 году он обратился к Я. Штйнеру с просьбой дать геометрическое доказательство одного из признаков равнобедренного треугольника. В последующем эта теорема получила название – Теорема Штейнера-Лемуса.

Если в равнобедренном треугольнике равны две медианы или две высоты, или две биссектрисы, то такой треугольник равнобедренный.

Первые два признака доказываются просто. Однако последний или теорема о том, что треугольник имеющий две равные биссектрисы является равнобедренным доказать довольно сложно – это теорема Штейнера-Лемуса.

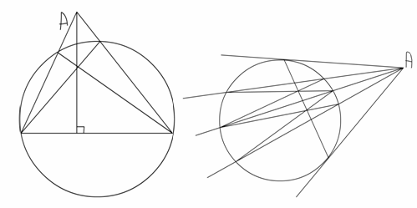
Если на плоскости нарисован круг с отмеченным центром. То любое построение выполняемое циркулем и линейкой можно выполнить только линейкой, что было доказано в 1833 году Штейнером.

Показано два построения такого рода из точки А проведены касательные к кругу и перпендикуляр к его диаметру (в этих построениях центр круга не нужен) другими словами, если задачу можно решить с помощью циркуля и линейки.

Познавательно о обучении:

Основные приоритеты в области биологического образования
Новая социокультурная ориентация школьной биологии предполагает развитие у учеников творческих способностей. Для этого необходимо ознакомление с самой структурой знаний, построение философско-методологических и теоретических стержней, обеспечивающих поиск проблем, открытия, озарения, интеллектуальн ...

Определение таких понятий, как "учебная деятельность", "активизация учебной деятельности", особенности учебной деятельности младших школьников
Термин " учебная деятельность " сравнительно не нов в психологии и педагогике. Уже в 40-х гг. им воспользовались довольно деятельно. Можно сослаться на одну из сверкающих работ А. Н. Леонтьева " К вопросцу о сознательности учения " , написанную в 1944 г.; базовый труд известного ...

Понятие и сущность формирования грамматически правильной речи, особенности усвоения детьми грамматической стороны речи
На этапах дошкольного возраста решаются важнейшие задачи речевого развития: обогащение словаря, воспитание звуковой культуры речи, формирование грамматического строя, развитие связной речи. Термин «грамматика» употребляется в языкознании в двух значениях: он обозначает, во-первых, грамматический ст ...