Обобщенная теорема синусов

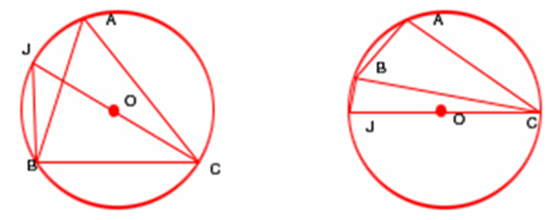
Теорема 1.1: Для треугольника АВС с радиусом описанного круга R выполнены соотношения:

.

Теорема Чевы

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой. Спутниковый мониторинг mssgloanss.ru. Спутниковая система мониторинга транспорта GPS в Москве.

Теорема 2.1: Если три чевианы AX, BY, CZ (по одной из каждой вершины) треугольника АВС конкурентны, то:

.

Три прямые (или отрезка) конкурентны, если все они проходят через одну точку.

Площади треугольников с равными высотами пропорциональны основаниям треугольников.

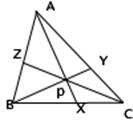
Ссылаясь на рисунок, имеем:

Аналогично:

Если их перемножить, то получим:

Теорема, обратная к этой теореме, также верна:

Теорема 2.2: Если три чевианы AX, BY, CZ удовлетворяют нижеприведенное соотношение, то они конкурентны:

.

Чтобы это показать, предположим, что две первые чевианы пересекаются в точке Р, как и прежде, а третья чевиана, проходящая через точку Р, будет CZ`. Тогда по теореме 2.1: .

Но по предположению: .

Следовательно: .

Точка Z` совпадает с Z, т.е. отрезки AX, BY и CZ конкурентны.

Замечательные точки

Центр окружности, описанной вокруг треугольника. О – её обозначение. Она является точкой пересечения трех перпендикуляров, делящих пополам стороны треугольника. R – радиус описанной окружности.

Чевианы, которые связывают вершины треугольника с серединами противоположных сторон, называются медианами. На рисунке отрезки АА`, BB` и CC` – медианы, так что |BA`|=|A`C|, |CB`|=|B`A| и |AC`|=|C`B|. Применяя теорему 2, делаем вывод, что медианы конкурентны. Их общая точка G называется центроидом треугольника. Если бы треугольник был вырезан из однородного материала, то он оставался бы в равновесии, будучи подвешенным в этой точке. Другими словами, центроид есть «центр тяжести» треугольника.

Теорема 3.1: Треугольник делится своими медианами на шесть меньших треугольников равной площади.

Теорема 3.2: Медианы треугольника делят одна другую в отношении 2:1. Другими словами, каждая медиана отсекает треть другой медианы.

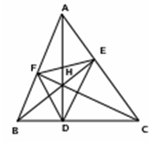
Чевианы AD, BE, CF, перпендикулярные прямым BC, CA, AB, соответственно, называются высотами треугольника АВС. Теорема, обратная теореме Чевы, устанавливает их конкурентность. Их общая точка Н называется ортоцентром.

Сами точки D, E, F называются основаниями высот. Соединяя их попарно, мы получим треугольник DEF – ортотреугольник треугольника АВС.

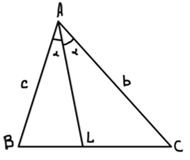
Другое важное семейство чевиан образуют биссектрисы внутренних углов. На рисунке показана одна такая биссектриса AL. Применяя теорему 1 к двум треугольникам ABL и ALC (углы которых в точке L, равные синусы), мы получаем:

.

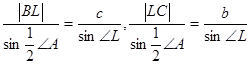Так как можем получить аналогичные результаты для биссектрис внутренних углов B и C, то таким образом доказали теорему.

Теорема 3.3: Каждая биссектриса внутреннего угла в треугольнике делит противоположную сторону на отрезки, длины которых пропорциональны длинам прилегающих сторон.

Любая точка на прямой AL равноудалена от прямых CA и AB. Аналогично, любая точка на биссектрисе внутреннего угла В равноудалена от прямых ВА и ВС. Следовательно, точка I, в которой эти две биссектрисы пересекаются, находится на равных расстояниях r от трех сторон:

Познавательно о обучении:

Психолого-педагогическая характеристика детей дошкольного возраста с ЗПР
Понятие "задержка психического развития" употребляется по отношению к детям со слабо выраженной недостаточностью центральной нервной системы - органической или функциональной. У этих детей нет специфических нарушений слуха, зрения, опорно-двигательного аппарата, тяжелых нарушений речи, он ...

Экспериментальная система работы по изучению темы: «Имя прилагательное. Родовые окончания имён прилагательных»
Формирование понятия об имени прилагательном начинается с повторения знаний учащихся о признаках предмета. Для этого учащиеся под руководством учителя устанавливают, что каждый предмет имеет не один, а несколько признаков, что признаки характеризуют предметы с разных сторон, что один и тот же призн ...

Экологическое воспитание детей среднего дошкольного возраста
Дошкольники пятого года жизни отличаются от малышей физическими и психическими возможностями: они увереннее во всех проявлениях, владеют первоначальными навыками самостоятельности, имеют более устойчивое внимание, более развитые восприятие и мышление, лучше понимают и воспроизводят речь взрослого, ...