Обобщенная теорема синусов

Теорема 3.4: Биссектрисы трех внутренних углов треугольника конкурентны.

Окружность с центром в точке I и радиуса r касается всех трех сторон и поэтому является вписанной окружностью.

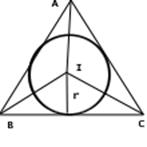
Вписанная и вневписанная окружности

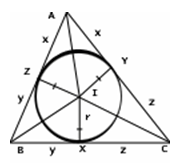
На рисунке изображена вписанная окружность, касающаяся сторон ВС, СА и АВ в точках X, Y, Z. Так как две касательные к окружности, проведенные из внешней точки, равны, то получаем, что |AY|=|AZ|, |BZ|=|BX|, |CX|=|CY|. На рисунке длины этих отрезков обозначены x, y, z так что y+z=a, z+x=b, x+y=c.

Складывая эти равенства и используя введенное Эйлером обозначение s для полупериметра (от «semiperimetr»), получим 2x+2y+2z= a + b + c=2s, поэтому x + y + z=s, т.е. справедлива.

Теорема 4.1: Для треугольника, изображенного на рисунке, выполняются соотношения:

x=s-a,

y=s-b,

z=s-c.

Так как треугольник IBC имеет основание равное а, высоту r, то его площадь равна: Прибавив к нему аналогичные выражения для и мы получим: следовательно, теорема доказана.

Теорема 4.2: Для треугольника, изображенного на рисунке, выполняется соотношение:

SABC = sr.

На рисунке изображен треугольник , стороны которого являются биссектрисами внешних углов треугольника АВС. Любая точка на биссектрисе угла В равноудалена от прямых АВ и ВС. Аналогично: любая точка на прямой равноудалена от прямых ВС и СА.

Следовательно, точка I, в которой эти биссектрисы пересекаются, находится на одинаковом расстоянии r от всех трех сторон. Так как I равноудалена от сторон АВ и АС, то она должна принадлежать множеству точек, равноудаленных от этих прямых, то есть она должна лежать на прямой А1, внутренней биссектрисе угла А.

Теорема 4.3: Внешние биссектрисы любых двух углов треугольника конкурентны с внутренней биссектрисой третьего угла.

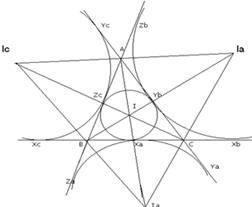
Окружность с центром в точке I радиуса r, касающаяся всех трех сторон треугольника, является одной из трех вневписанных окружностей. Каждая из вневписанных окружностей касается одной из сторон треугольника внутри, а двух других сторон (продолженных) извне.

Обозначив точки касания как на рисунке, две касательные из одной точки к окружности имеют одинаковые длины, то: ;

Следовательно, касательная из точки В (или любой другой вершины) к вневписанной окружности, расположенной за противолежащей стороной, имеет длину s. Действительно: .

Кроме того, так как: .

И так далее, то также и: .

3.5 Теорема Штейнера-Лемуса

Теорема 5.1: Любой треугольник, у которого равны длины биссектрис двух углов (измеряемые от вершины до противоположной стороны), является равнобедренным.

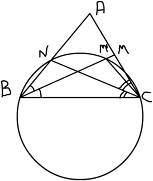
Одно из простейших доказательств этой теоремы опирается на следующие две леммы:

Лемма 5.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершинами на окружности.

Познавательно о обучении:

Краткая характеристика организации ДОУ №10
Муниципальное образовательное учреждение №10 расположено по адресу: Свердловская область, г. Красноуфимск, ул. Свободы, 60. Основан детский сад в 1975 году. Педагогический коллектив ДОУ №10 города Красноуфимск стабильный: 90% педагогов работают в детском саду более пяти лет, из них 11 имеют высшую ...

Проблемно-поисковый урок русского языка
Проблема: бедность, невыразительность речи учащихся, низкая грамотность. Концептуальная цель изучения русского языка (согласно рабочей программе по предмету): постижение богатства и значимости русского языка, формирование речевой культуры, повышение уровня грамотности. Тема: Глагол и его употреблен ...

Система работы по формированию начал экологической культуры у детей младшего дошкольного возраста в процессе познавательной деятельности
МДОУ №110 «Дубравушка» работает по программе «Сообщество». В соответствии с требованиями программы, занятия проходят в форме утренних сборов. На утренних сборах даются знания на основе задач из «программы воспитания ребенка-дошкольника». Главное отличие программы «Сообщество», которое отличает ее о ...