Применение софизмов на уроках математики

Итак, площадь фигуры, ограниченной синусоидой и осью Ох, равна нулю. Но площадь фигуры между некоторой кривой и осью Ох, может равняться нулю только в том случае, если эта кривая совпадает с осью Ох. Следовательно, график функции синус совпадает с осью Ох.

Раскрытие софизма:

Здесь допущена ошибка при интегрировании синуса. При вычислении с помощью интегрирования площади фигуры, заключенной между осью Ох и некоторой кривой, необходимо учитывать, что площадь при этом получается со знаком «плюс» или «минус». Это означает, что если кривая расположена над осью Ох, то площадь имеет знак «плюс», а если под осью Ох – знак «минус».

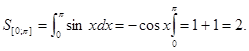Синус на отрезке [0; ] положителен, а на отрезке [] . Отрицателен. Поэтому площадь фигуры, заключённой между синусоидой и осью Ох, на отрезке [0; ] равна , а на отрезке [] площадь равна .

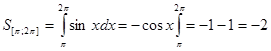Тогда площадь , на отрезке [0; 2] будет равна , а на отрезке [0; 2n] составит .

Софизмы могут самые разные и приведённая система подтверждает, что софизмы могут быть использованы и в соответствии с тематикой обучения, т.е. можно подобрать софизм, который будет актуален при проведении урока по различным темам. Конечно, разумно использовать софизм после изучения конкретной темы, например в 7 классе после темы «Формулы сокращённого умножения», или в 10 классе при изучении темы «Логарифмы», т.к. решение некоторых софизмов можно свести к тем же логарифмам или решить его, используя формулы сокращённого умножения.

Проработав соответствующую психолого-педагогическую и методическую литературу по данному вопросу, очевидно, сделать вывод о том, что критичность является важным качеством мышления, развитие которого требует значительных усилий со стороны учителя математики. Кроме того, полезно развивать критичность мышления, в процессе обучения, отступая от стандартных методов проведения урока.

Бесспорно, достичь поставленной цели с помощью только стандартных задач невозможно. Если учитель математики «заполнит отведённое ему время натаскиванием учащихся в шаблонных упражнениях, он убьёт их интерес, затормозит их умственное развитие». С помощью нестандартных задач интенсивнее формируется интерес и достигается цель углубления. Поиск решения нестандартных задач является прекрасным средством развития критического мышления, строгости суждений и математического вкуса. Одним из таких средств является использование софизмов на уроках математики.

Конечно, не следует, и преувеличивать роль софизмов в развитии критичности мышления. Они ни в коем случае не должны доминировать над обычными, традиционными упражнениями. Но как раз своей не стандартностью они «помогут» решить проблему заинтересованности в обучении, а если правильно организовать процесс внедрения софизмов в ход урока, то во многом облегчится задача развития критичности мышления, потому, что софизмы относятся к типам заданий, решение которых основано на рассмотрении различных ситуаций. При регулярном использовании софизмов на уроках у учеников вырабатывается своеобразная «подозрительность», что естественно указывает на хорошо развитую критичность мышления. Причём, софизмы универсальны в обучении тем, что подходят для учащихся всех возрастов.

Познавательно о обучении:

Психолого-педагогические аспекты формирования лексической стороны речи детей дошкольного возраста
Дошкольное образовательное учреждение – первое и самое ответственное звено в общей системе народного образования. Овладение родным языком является одним из самых важных приобретений ребенка в дошкольном детстве. Именно дошкольное детство особенно сенситивно к усвоению речи. Поэтому процесс речевого ...

Паспорт общеобразовательного учреждения
Тип и вид образовательного учреждения – Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №167. Адрес – 663690, Россия, г. Зеленогорск Красноярского края, ул. Набережная, 14. Директор школы – Черников Борис Сергеевич. Телефон – 3–44–13. Школа в своей деятельности руков ...

Особенности форм устройства детей-сирот и детей, оставшихся без попечения родителей в Российской Федерации
Семейным законодательством Российской Федерации предусмотрены несколько форм устройства детей-сирот и детей, оставшихся без попечения родителей – это усыновление, опека (попечительство), приемная семья, устройство в государственные учреждения. Этот список не полный, так как законодатель дает возмож ...