Серединный треугольник и прямая Эйлера

Планирование занятий

Обобщенная теорема синусов

Теорема синусов – это тригонометрическая теорема, которой мы будем часто пользоваться.

К сожалению, в учебниках она обычно появляется в урезанной форме, и в этом виде она не приносит всей той пользы, которую могла бы дать обобщенная теорема. Поэтому докажем эту теорему в желательной для нас форме.

Давайте вспомним формулировку теоремы синусов, о чем в ней говориться?

Учащиеся формулируют известную им теорему синусов (если требуется, то с помощью учителя).

Формулировка: стороны треугольника пропорциональны синусам противолежащих углов:

.

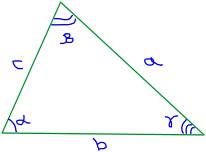
Мы начинаем с треугольника АВС и описываем вокруг его окружность с центром в точке О и радиусом R, как показано на рисунке. Проведем диаметр CJ и хорду BJ.

Что можно сказать про угол CBJ?

Он прямой.

Почему?

Потому что он вписан в окружность и опирается на диаметр.

Да, в обоих случаях ÐCBJ – прямой, так как он вписан в полукруг.

Следовательно, как тогда можно выразить sinÐJ?

Рассмотрим рисунок.

Что вы можете сказать про углы J и A, какие они?

Они равны.

Почему?

Потому что они опираются на одну и ту же дугу окружности.

На рисунке ÐJ=ÐA, поскольку углы J и A опираются на одну и ту же дугу окружности.

А на втором рисунке, что вы можете сказать про углы J и A, какие они?

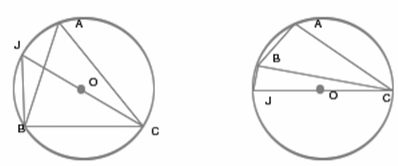
Скажите, вот вы сделали дополнительные построения, какую фигуру вы видите на рисунке.

Треугольник.

Скажите, какие дополнительные построения вы сделали?

Вокруг имеющегося треугольника мы описали окружность, построили диаметр CJ и хорду BJ.

Какая в итоге получилась фигура?

Четырехугольник, вписанный в окружность.

Так что можно сказать про углы J и A данного четырехугольника, какие они?

Противоположные.

А что вам известно про противоположные углы вписанного четырехугольника?

Они являются дополнительными.

Что это значит? Какой можно из этого сделать вывод? Как это можно записать?

ÐJ = 1800 – ÐА

Давайте посчитаем синус ÐJ.

sinÐJ = sin(1800 – ÐА)

А это почему?

Потому что противоположные углы вписанного четырехугольника являются дополнительными.

И что из этого следует? Какой можно сделать вывод? Чему же равен sinÐJ?

sinÐJ=sinÐA

Чем вы воспользовались, чтобы получить это равенство?

Мы воспользовались равенством sin q = sin (1800 – q).

Скажите, этот вывод относится к какому рассматриваемому случаю, 1 или 2?

К обоим.

Почему к обоим?

Потому что данное равенство sin q = sin (1800 – q) справедливо для этих двух случаев.

Теперь на основании сделанных умозаключений давайте сделаем вывод, что sinÐA = a/2R, так как sin q = sin (1800 – q), и получим что a/sinÐA=2R.

Аналогично, если проведем подобные рассуждения, получим такие же результаты для остальных углов.

Объединяя результаты, мы можем сформулировать обобщенную теорему синусов следующим образом:

Запишем обобщенную теорему синусов.

Теорема 1.1: Для треугольника АВС с радиусом описанного круга R выполнены соотношения:

a / sinÐA = b / sinÐB = c / sinÐC = 2R.

Решение задач:

Приведенные ниже задачи разделены на 2 блока. Задачи из блока 1 – это задачи на применение теоремы синусов, задачи из блока 2 – задачи на применение обобщенной теоремы синусов.

Задачи блока 1 можно предложить для решения учащимся до введения нового материала.

Блок 1.

1. С помощью теоремы синусов решите треугольник, если:

а) ÐА=600, ÐВ=400, с =14

б) ÐА=300, ÐС=750, b = 4,5

в) ÐА=800, a = 16, b = 10

г) ÐB=450, ÐC=700, a = 24,6

д) ÐА=600, a = 10, b = 7

2. В треугольнике АВС АС=12, ÐА=750, ÐС=600. Найдите АВ и SABC.

3. Найдите стороны треугольника АВС, если ÐА=450, ÐВ=300, а высота AD равна 3 метрам.

4. В параллелограмме . Найдите ÐBDC и ÐDBC.

Познавательно о обучении:

Особенности проведения занятий при эндокринных заболеваниях
Необходимо учитывать следующие особенности состояния организма при организации физической подготовки: нарушение всех видов обмена (в том числе водного, минерального и витаминного) при преимущественном нарушении одного из них; ослабление силы и тонуса мышц; функциональная слабость всех систем и орга ...

Обзор образовательной программы по экологическому воспитанию для детей дошкольного возраста
Развитие экологического образования как нового направления дошкольной педагогики в нашей стране началось гораздо позже, чем экологического образования школьников и студентов. Несмотря на это, в настоящее время именно дошкольное звено в системе непрерывного экологического образования работает наибол ...

Методические рекомендации по использованию наглядного моделирования на занятиях по развитию речи с детьми старшего дошкольного возраста
Дошкольное образование – это первая ступень в системе образования, поэтому основная задача педагогов, работающих с дошкольниками – формирование интереса к процессу обучения и его мотивации, развитие и коррекция речи. Сегодня совершенно определенно можно выявить назревшие противоречия между общим дл ...