Серединный треугольник и прямая Эйлера

5. Найдите биссектрисы треугольника, если одна из его сторон равна а, а прилежащие к этой стороне углы равны и .

Блок 2. Как правильно выбрать шторы для зала.

6. Найдите угол А треугольника АВС, если известно, что радиус описанной около этого треугольника окружности равен 6, а сторона ВС равна 3.

7. Найдите сторону ВС треугольника АВС, если известно, что угол А равен 70 градусам и радиус описанной окружности равен 4.

8. Найдите радиус описанной около треугольника окружности, если одна его сторона равна 4, противоположный ей угол равен 55 градусам.

Домашнее задание:

Учить новый материал.

Задачи: Придумать 3 задачи на применение обобщенной теоремы синусов.

Сделать доклад на тему: «Джованни Чева – его теоремы и тд.»

Так же нужно вспомнить, как связаны площади треугольников с равными высотами и их основания.

Задание «Сделать доклад» дается 2 группам учащихся (каждая группа состоит максимум из 3 человек), предполагается соревновательная форма работы.

Теорема Чевы

Этап 1. Организационный момент. Проверка домашнего задания. Повторение изученного материала.

Этап 2. Введение нового материала.

Вы уже хорошо знакомы с понятием треугольник. Давайте вспомним, какие линии в треугольнике вам известны?

Учащиеся перечисляют известные им линии треугольника. Особое внимание учитель обращает на медиану, высоту и биссектрису. Далее учитель просит учащихся проанализировать эти три линии и найти их общие черты и различия. Учащиеся должны увидеть, что каждая из этих линии это отрезок, выходящий из вершины треугольника, соединяющий вершину с точкой на противоположной стороне.

Вводится определение.

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой.

Краткая историческая справка.

Этот термин происходит от имени итальянского математика Джованни Чевы, который в 1678 году опубликовал следующую очень полезную теорему:

Учащиеся записывают

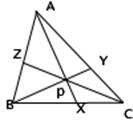
Теорема 2.1: Если три чевианы AX, BY, CZ (по одной из каждой вершины) треугольника АВС конкурентны, то:

.

Когда мы говорим, что три прямые (или отрезка) конкурентны, то имеем в виду, что все они проходят через одну точку, которую обозначим через Р.

Как результат выполненного домашнего задания учащиеся под руководством учителя формулируют факт о том, что площади треугольников с равными высотами пропорциональны основаниям треугольников.

Для доказательства этой теоремы (как только что было уточнено) вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников.

Далее, путем построения простой логической цепочки рассуждений ученики выводят следующие факты:

Для доказательства справедливости утверждения теоремы классу предлагается проверить ее утверждение, используя уже полученный результат.

Классу сообщается, что теорема, обратная к этой теореме, также верна.

Ученикам предлагается сформулировать теорему обратную к исходной. Ученики формулируют и записывают:

Теорема 2.2: Если три чевианы AX, BY, CZ удовлетворяют нижеприведенному соотношению, то они конкурентны:

.

Доказательство этой теоремы можно предложить ученикам выполнить дома, в случае, если на дом ученикам дается другое задание, то доказательство можно провести на занятии. В зависимости, от планов учителя, доказывать теорему могут ученики или он сам.

Решение задач:

Следующим этапом предлагаются задачи с нарастающей трудностью:

Доказать, что в треугольнике АВС в одной точке пересекаются:

1. медианы треугольника

2. биссектрисы внутренних углов треугольника

3. высоты треугольника

4. прямые, выходящие из вершины треугольника с точками касания вписанной в него окружности

Познавательно о обучении:

Игра – сфера жизни детей. Игра – активная познавательно - развивающая деятельность детей
Что наша жизнь? Игра… Сущность понятия «педагогическая игра» Игровые технологии в младшем школьном возрасте Игровые технологии в среднем и старшем школьном возрасте Игры детей – творческий процесс, инструмент самореализации и самоутверждения детей, путь свободного решения игровой проблемы и свободн ...

Механизмы реализации игрового сюжета
Погружение в сюжет происходит через : Театрализованные представления (открытие смены – прибытие Звездного десанта в Город Звезд; во всех мероприятиях поддерживается игровой сюжет через участие в них главных действующих лиц – Мэра, Советника, Председателя городской Думы, Астролога, Звездочетов, дире ...

Роль педагогических инноваций в современном образовании
В данном параграфе будут раскрыты разнообразные подходы к типологии педагогических инноваций, так как они отражают понимание учеными и педагогами - практиками в разное время сущностного значения инноваций в образовании, той роли, которую они им отводили. Общепринятой типологии или классификации нов ...