Серединный треугольник и прямая Эйлера

В силу того, что теоретическая часть этого занятия носит исключительно ознакомительный характер, то на этапе решения задач предполагается решение задач подготавливающих к введению нового материала следующего занятия и повторение ранее изученного материала.

Решение задач:

1. Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке, которая называется ортоцентром треугольника.

2. В остроугольном треугольнике АВС проведены высоты Докажите, что треугольники подобны треугольнику АВС.

3. Треугольник , вершинами которого являются основания высот треугольника АВС. Найдите углы ортоцентрического треугольника остроугольного треугольника АВС, если углы треугольника АВС равны А, В, С.

4. Докажите, что высоты остроугольного треугольника являются биссектрисами его ортоцентрического треугольника.

5. Найдите углы ортоцентрического треугольника тупоугольного треугольника, если углы треугольника АВС равны А, В, С (угол С тупой).

6. Найдите углы всех треугольников, которые подобны своим ортоцентрическим треугольникам.

7. Дан остроугольный треугольник АВС. Докажите, что точки, симметричные ортоцентру треугольника АВС относительно его сторон, лежат на окружности, описанной около этого треугольника.

8. Продолжения высот остроугольного треугольника АВС пересекают описанную окружность в точках. Докажите, что а) треугольник подобен ортоцентрическому треугольнику треугольника АВС и коэффициент подобия равен 2, б) высоты треугольника АВС являются биссектрисами треугольника .

9. Пусть Н – ортоцентр треугольника АВС. Докажите, что радиусы окружностей, описанных около треугольников АВН, ВСН и САН равны между собой и равны радиусу окружности, описанной около треугольника АВС.

Домашнее задание:

Решить задачи 6-9 и дорешать задачи из классной работы.

Подготовить доклад на тему «Ортотреугольник»

Ортотреугольник

Этап 1. Проверка домашнего задания и разбор не решенных задач.

Этап 2. Повторение ранее изученного материала.

Этап 3. Введение нового материала (объяснительно иллюстративный метод).

Прежде всего, учащиеся формулируют определение ортоцентра треугольника и ортоцентрического треугольника. Далее учащиеся записывают формулировку теоремы.

Теорема 6.1: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

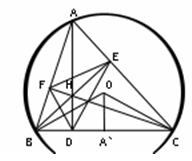
Одно из простейших доказательств опирается на две следующие леммы:

Две следующие леммы, используемые для доказательства теоремы 6.1 уже хорошо известны учащимся из курса планиметрии.

Лемма 6.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают равные углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно; меньший угол с вершиной на окружности.

Лемма 6.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

Доказательство:

Пусть АВС – треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки ВМ и CN делят пополам углы В и С. Мы хотим доказать, что . Возьмём точку М` на отрезке ВМ так, чтобы . Так как этот угол равен углу M`BN, то четыре точки N, B, C, M` лежат на одной окружности. Поскольку то . По лемме 1.6.1 . Следовательно,

Познавательно о обучении:

Особенности обучения письму и чтению детей в условиях билингвального образования
Письмо и чтение представляют собой сложнейшие интегративные навыки, формирование которых проходит ряд общих стадий, связанных с включением в деятельность практически всех сенсорных систем и всех структур мозга. На начальных этапах обучения (аналитическом и синтетическом) происходит формирование той ...

Приёмы создания благоприятного психологического климата в коллективе. Понятие конфликта как столкновения, отражающего создавшиеся противоречия
Ничто так не оказывает превосходство характера, как хорошее поведение в ссоре, которой нельзя избежать. Г. Тейлор, английский поэт 1. Создания благоприятного психологического климата в коллективе Сущность понятия «конфликт» Сигналы конфликтов Формы конфликтов Способы разрешение конфликта Избегание ...

Применение радио и звукозаписи в работе с детьми
Использование радио в учебной работе детских садов открывает широкие возможности повышения эффективности воспитания и обучения, всестороннего воздействия на личность дошкольника. Центральное радио ежедневно транслирует передачи для дошкольников, которые с успехом можно использовать в учебной работе ...