Серединный треугольник и прямая Эйлера

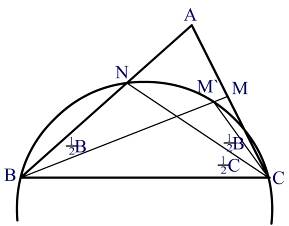
Доказательство теоремы 6.1:

При доказательстве этой теоремы важно обратить внимание учащихся на построении структуры логических рассуждений, которые делают доказательство данной теоремы более коротким.

Часто случается, что теорема может быть выражена в форме «противоположной к обратной» – эквивалентной первоначальной.

Например, вместо того, чтобы сказать: «Все люди смертны», мы можем также сказать «Бессмертные не есть люди».

Вместо доказательства самой теоремы 6.1. нам достаточно доказать, что если в треугольнике АВС: , то . Но это есть прямое следствие леммы 6.1.2.

Теорема 6.2: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Учащимся предлагается самостоятельно показать доказательство этой теоремы дома.

Мы уже отметили на рисунке, что . А так как отрезок HD перпендикулярен отрезку DB, то и отрезок FD должен быть перпендикулярен отрезку OB. Перпендикулярность отрезков DE и OC, а также EF и OA показывается аналогично.

Решение задач:

Задачи 1-7 из задачника.

Домашнее задание:

Решить задачи 8-11 из задачника.

Этап 1. Проверка домашнего задания. Особое внимание уделяется проверке доказательства теоремы 6.2.

Этап 2. Повторение ранее изученного материала. Проводится сначала письменный опрос учащихся по материалу предыдущих уроков. После окончания работы ученики сдают листочки со своими ответами, и начинается устный опрос по тем же самым вопросам, что дает возможность учащимся проверить их работы.

Этап 3. Введение нового материала.

Учащиеся записывают определение:

Треугольник, полученный соединением середин сторон данного треугольника, назовем серединным треугольником.

На доске по заготовленному за ранее чертежу ведется объяснение.

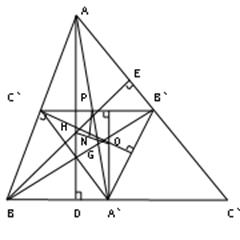
На рисунке A`B`C` есть срединный треугольник треугольника АВС. Рассмотрим так же две медианы AA` и BB`, пересекающиеся в точке G, две высоты треугольника ABC, пересекающиеся в точке H, и две высоты треугольника A`B`C` пересекающиеся в точке O.

Что вы можете сказать про треугольники АВС и А`B`C`? Какие они?

Стороны треугольника A`B`C` параллельны сторонам треугольника АВС, поэтому эти треугольники подобны.

Далее, |C`B`|=1/2|BC|, поэтому отношение длин любых двух соответствующих отрезков (а не только соответствующих сторон) будет равно1:2. В действительности, отрезки B`C`, C`A`, A`B` разбивают треугольник ABC на четыре конгруэнтных треугольника. Кстати, точка P –середина отрезка B`C` – также является и серединой отрезка AA`

Далее мы видим, что AC`A`B` – параллелограмм, следовательно, прямая AA` делит пополам отрезок B`C`. Поэтому медианы треугольника A`B`C` лежат на медианах треугольника ABC, а это значит, что оба треугольника имеют один и тот же центроид G.

Высоты треугольника A`B`C`, изображенные на рисунке, являются срединными перпендикулярами сторон AB и BC треугольника ABC. Отсюда делаем вывод, что точка O – ортоцентр треугольника A`B`C` – является время и центром окружности, описанной вокруг треугольника ABC.

Так как точка H – ортоцентр треугольника ABC, а точка O – ортоцентр подобного ему треугольника A`B`C`, то |AH| = 2 |OA`|. По теореме 3.2 |AG| + 2 |GA`|. И так как оба отрезка, AD и OA`, перпендикулярны стороне BC, то они параллельны. Следовательно,

ÐHAG = ÐOA`G, Ñ HAG ¥ Ñ OA`G и ÐAGH = Ð A`GO.

Этим показано, что точки O, G, H коллинеарны и |HG| = 2 |GO|, то есть справедлива

Теорема 7.1: Ортоцентр, центроид и центр описанной окружности произвольного треугольника лежат на одной прямой. Центроид делит расстояние от ортоцентра до центра описанной окружности в отношении 2:1.

Решение задач:

№55 из задачника.

Домашнее задание:

Учить все определения и теоремы.

Окружность девяти точек

Рассмотрим рисунок. На нем точки K, L, M – середины отрезков AH, BH, CH, лежащих на высотах.

Познавательно о обучении:

Чтение как процесс усвоения
Читатель не поглощает материал пассивно, как контейнер или губка. Это звучит банально, но вплоть до последнего времени авторитарные методы обучения, построенные на принципе кувшина и бутылки, господствовали в школе и за ее пределами, а традиция умирает медленно. Уважающий себя, независимый человек ...

Описание примерной программы занятий для развития мышления старших дошкольников средствами нетрадиционного рисования
Цикл занятия проводился в течение месяца с экспериментальной группой состоящей из 10 человек 4 мальчика и 6 девочек, 2 раза в неделю по 25-30 минут. Общее количество занятий -10. Исследовательская работа проводилась по плану экспериментальной работы: констатирующий, формирующий и контрольный этапы, ...

Педагогические методы и приёмы стимулирования учебно-познавательной деятельности учащихся
Стимулом в психологии называют внешнее побуждение человека к активной деятельности. Поэтому стимулирование - это фактор деятельности учителя. В самом названии «методы стимулирования и мотивации» находит отражение единство деятельности учителя и учащихся: стимулов учителя и изменение мотивации школь ...