Серединный треугольник и прямая Эйлера

Обозначив точки касания как на рисунке, т.к. две касательные из одной точки к окружности имеют одинаковые длины, то: ;

Следовательно, касательная из точки В (или любой другой вершины) к вневписанной окружности, расположенной за противолежащей стороной, имеет длину s. Действительно: .

Кроме того, так как: .

И так далее, то также и: .

Решение задач:

1. Пусть М – точка на стороне АС треугольника АВС. Обозначим через R1 и R2 радиусы окружностей, описанных около треугольников АВМ и СВМ соответственно. Докажите, что R1 относится к R2, как АВ к ВС.

2. Даны окружность и точка А вне ее. АВ и АС – касательные к окружности (В и С – точки касания). Докажите, что середины двух дуг, на которые разделена данная окружность точками В и С, являются центром вписанной и вневписанной окружности треугольника АВС.

3. Пусть J – центр окружности, вписанной в треугольник АВС, Ja – центр вневписанной окружности (касающейся сторон ВС и продолжений сторон АВ и АС). Докажите, что точки В, С, J, Ja – расположены на одной прямой.

4. Пусть J – центр окружности, вписанной в треугольник АВС. Докажите, что прямая AJ проходит через центр окружности, проходящей через точки В, С и J.

5. Пусть Ja – центр вневписанной окружности. Найдите угол AJaB, если угол АВС равен b.

6. Три окружности радиусам 1, 2, 3 попарно касаются друг друга внешним образом. Найдите радиус окружности, проходящей через точки касания этих окружностей.

Домашнее задание:

Решить задачи 5-6 и доделать задачи из классной работы.

Сделать доклад о Штейнере и Лемусе.

Теорема Штейнера-Лемуса

Этап 1. Проверка домашнего задания.

Этап 2. Повторение ранее изученного материала.

Учащиеся формулируют определения и теоремы, изученные на прошлых уроках.

Этап 3. Введение нового материала (объяснительно иллюстративный способ).

Учащиеся рассказывают подготовленную историческую справку о Штейнере и о Лемусе.

Ученики записывают формулировку теоремы.

Теорема 5.1: Любой треугольник, у которого равны длины биссектрис двух углов (измеряемые от вершины до противоположной стороны), является равнобедренным.

Одно из простейших доказательств этой теоремы опирается на следующие две леммы:

Лемма 5.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух не равных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершинами на окружности.

Учащиеся дома должны записать это доказательство в символьной форме

Лемма 5.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

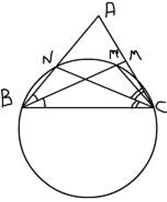
Доказательство: Пусть АВС – треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки BM и CN делят пополам углы В и С. Мы хотим доказать, что |BM|>|CN|. Возьмем точку М` на отрезке ВМ так, чтобы ÐM`CN=1/2 ÐB. Так как это угол равен углу M`BN, то четыре точки N, B, C, M` на одной окружности. Поскольку ÐB < 1/2(ÐB+ÐC) < 1/2(ÐA+ÐB+ÐC), то ÐCBN < M`CB <90°.

По лемме 5.1.1 |CN|<|M`B|. Следовательно, |BM|>|BM`|>|CN|.

Доказательство теоремы: Часто бывает, что теорема может быть выражена в форме «противоположной к обратной» – эквивалентной к обратной. Вместо доказательства теоремы 5.1 для нас будет достаточно доказать, что если в треугольнике АВС: В ¹ С, то |BM| ¹ |CN|. Но это есть прямое следствие леммы 5.1.2.

Познавательно о обучении:

Анализ и интерпретация результатов социально-психологического исследования
Для исследования нами были отобраны две выборки студентов АУЦА: первая группа была представлена студентами 4 курса факультета менеджмента, в чьих занятиях проводились имитационные игры. Вторая группа – это студенты 4 курса факультета журналистики, у них имитационные игры в процессе обучения не испо ...

Научно-методические основы использования средств ИКТ в образовании
Глубокие социальные перемены, происходящие в современном обществе, требуют новых подходов к развитию образования, изменения методологии и парадигмы педагогической науки. Материалистическая теория познания перестали служить методологической основой педагогической науки и других наук в целом. Методол ...

Формы работы по патриотическому воспитанию детей в современной школе
Формирование патриотических качеств личности – это целенаправленный, специально организуемый процесс. Патриотические качества – это качества личности, характеризующие ее способность к активному проявлению гражданской позиции. Формирование их возможно лишь через вовлечение подростка в специфическую ...